 Descrivere geometricamente un oggetto significa averne interpretato la forma e misurato le sue dimensioni e riprodurlo poi graficamente sul di un supporto quale il foglio o lo schermo di un computer. Misurare un oggetto, vuol dire descriverlo in modo che sia quantificabile e confrontabile. Il concetto di misura è antico, basti pensare che lo scambio si fondava sulle comparazioni tra ciò che veniva ceduto e ciò che veniva acquistato. Per cui, i concetti di misura e di misurazione si sono sviluppati di pari passo con l’evoluzione umana, diventando con il tempo sempre più raffinati e variegati.
Descrivere geometricamente un oggetto significa averne interpretato la forma e misurato le sue dimensioni e riprodurlo poi graficamente sul di un supporto quale il foglio o lo schermo di un computer. Misurare un oggetto, vuol dire descriverlo in modo che sia quantificabile e confrontabile. Il concetto di misura è antico, basti pensare che lo scambio si fondava sulle comparazioni tra ciò che veniva ceduto e ciò che veniva acquistato. Per cui, i concetti di misura e di misurazione si sono sviluppati di pari passo con l’evoluzione umana, diventando con il tempo sempre più raffinati e variegati.
Nel disegno tecnico (architettonico e ingegneristico), la misurazione è parte fondamentale. Ogni tratto, ogni segno della matita sul foglio, è simbolo di un linguaggio universale. Un insieme di norme che codificano questi segni grafici dando loro un significato preciso e univoco. Ad esempio, linee spesse mettono in evidenza elementi importanti ed in primo piano, mentre linee tratteggiate descrivono elementi non visibili o di secondaria importanza.
Ma avviamoci in questo percorso che ci porta alla scoperta dei sistemi di misurazione.
SISTEMA METRICO DECIMALE
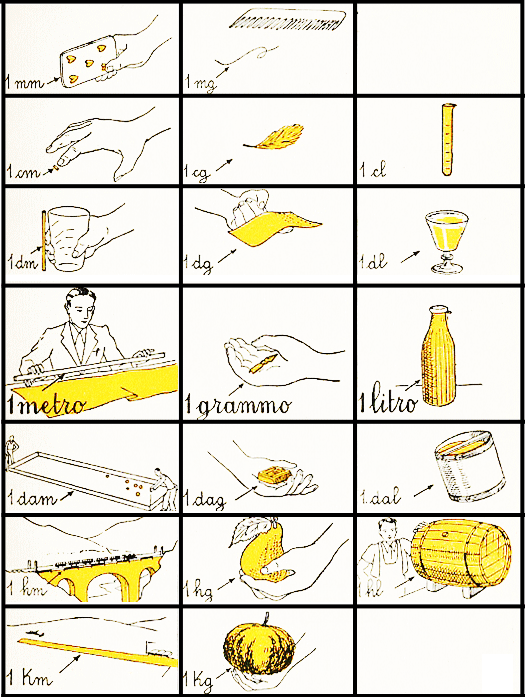 I Sistemi di misurazione, intesi come insieme di regole codificate, fanno per la prima volta la loro apparizione in Francia nel 1791 e la loro diffusione sarà capillare, prima nei paesi non anglosassoni e poi anche in quelli. L’Italia, come la maggior parte dei paesi mondiali, utilizza per misurare il Sistema Metrico Decimale basato su potenze di dieci, legato direttamente al sistema decimale dei numeri, legame che ne ha garantito il successo. Nei primi sistemi metrici, vi erano solo due unità di misurazione fondamentali, il metro per le lunghezze e il grammo per il peso. Tutte le altre unità di misurazione erano derivate da queste.
I Sistemi di misurazione, intesi come insieme di regole codificate, fanno per la prima volta la loro apparizione in Francia nel 1791 e la loro diffusione sarà capillare, prima nei paesi non anglosassoni e poi anche in quelli. L’Italia, come la maggior parte dei paesi mondiali, utilizza per misurare il Sistema Metrico Decimale basato su potenze di dieci, legato direttamente al sistema decimale dei numeri, legame che ne ha garantito il successo. Nei primi sistemi metrici, vi erano solo due unità di misurazione fondamentali, il metro per le lunghezze e il grammo per il peso. Tutte le altre unità di misurazione erano derivate da queste.
Pur esistendo differenti sistemi metrici di misurazione, usati in campo scientifico e nell’Unione Sovietica, oggi per far chiarezza ed uniformarli, è stato realizzato lo SI, acronimo che indica il Sistema Internazionale di unità di misura. Questo deriva dal sistema MKS (metro, kilogrammo, secondo) a cui sono state aggiunte altre 4 unità fondamentali quali il kelvin (temperatura), l’ampere (intensità di corrente elettrica), la candela (intensità luminosa) e la mole (quantità delle sostanze).
Per cui il Sistema Internazionale consta di due classi di unità ben definite:
- UNITA’ DI BASE (lunghezza, massa, temperatura, tempo, corrente elettrica, intensità luminosa, quantità di sostanza);
- UNITA’ DERIVATE (lavoro, energia, potenza).
SISTEMI NON METRICI
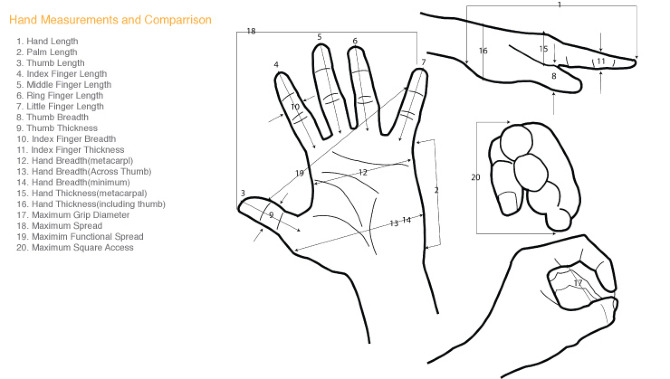
Sistema Imperiale Britannico
Come è facile constatare, nel mondo, esistono anche altri sistemi di misurazione, non accettati internazionalmente, ma altrettanto diffusi quali il Sistema Imperiale Britannico e il Sistema Americano entrambi derivati dalle antiche unità di misura inglesi. La loro diffusione è dovuta alla grande quantità di conquiste effettuate dall’inghilterra, da cui la loro estensione a tutti i paesi del Commonwealth e nei paesi dell’Impero britannico. Molto lentamente, anche questi paesi stanno procedento all’adozione del sistema metrico internazionale, già avvenuto in alcuni campi come tecnologia, medicina e scienza mentre ancora resistono quelle legate alla misurazione.
LA MISURAZIONE NEL DISEGNO TECNICO
|
L’importanza della misurazione ha il suo apice nel disegno tecnico, dove tutto è normato e dove tutto crea una relazione tra oggetti reali e la loro rappresentazione sulla carta. Nel disegno tecnico, sia esso architettonico, meccanico, urbanistico o cartografico, si dice che l’oggetto venga rappresentato in “scala”, intendendo per scala una relazione tra la misura reale dell’oggetto e la misura dello stesso nel disegno, utilizzando per entrambi la stessa unità di misura.
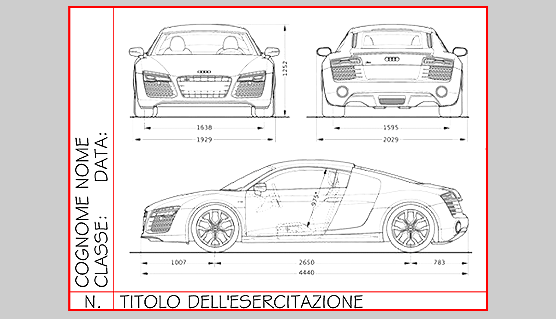
La prima operazione da effettuare, è la misurazione della dimensione dell’oggetto da rappresentare e le dimensioni del foglio sul quale sarà rappresentato. In parole povere, bisogna trovare il “miglior compromesso” tra la dimensione del supporto di rappresentazione (il foglio) e le dimensioni reali dell’oggetto. Immaginiamo di dover rappresentare su carta un’auto di grandi dimensioni come quella nell’immagine qui sotto:

sarà necessario misurare il lato di maggior dimensione dell’oggetto (auto), ossia la sua lunghezza e la dimensione del lato maggiore del nostro supporto da disegno (foglio):

Il foglio è evidentemente molto più piccolo. Dovremo, di conseguenza, ridurre l’oggetto per far si che esso sia rappresentabile con precisione entro i limiti del foglio.

Immaginiamo che l’auto misuri 4440 mm (444 centimetri) e sapendo che il lato maggiore del foglio è pari a 330 mm (33 centimetri), proviamo per tentativi a farla entrare nel foglio. Nella tabella sotto sono riportati alcuni esempi di riduzione:
| Misura Auto (mm) |
/ |
= |
Dimensione foglio (330 mm) |
Scala |
| 4.440 |
2 |
2.220 |
NO |
1:2 |
| 4.440 |
4 |
1.110 |
NO |
1:4 |
| 4.440 |
5 |
880 |
NO |
1:5 |
| 4.440 |
10 |
440 |
NO |
1:10 |
| 4.440 |
20 |
220 |
OK |
1:20 |
| 4.440 |
15 |
296 |
OK |
1:15 |
Nel primo caso abbiamo diviso per 2 la misura dell’auto, ma evidentemente non può entrare all’interno del foglio da disegno (colore rosso).
Nel secondo caso dividiamo per 4, ma anche così la misura dell’auto è maggiore della misura del foglio. Procedendo per tentativi aumentiamo il fattore di divisione. Dividendo per 20 l’auto rientrerebbe nel foglio (colore giallo). Ma in quest’ultimo caso, sarebbe rimasto molto spazio tra i suoi bordi e il disegno dell’auto; quindi, questa riduzione è eccessiva.
Nell’ultimo tentativo, dividendo per 15 la lunghezza dell’auto, abbiamo trovato il giusto compromesso tra oggetto e foglio (colore verde). Sotto una possibile rappresentazione grafica dell’auto in oggetto:
SCALA NUMERICA
Nell’ultima colonna della tabella precedente, è riportata la dicitura scala. Si tratta della cosiddetta scala numerica, ossia di un modo attraverso il quale indicare il grado di riduzione dell’oggetto. E’ espressa sotto forma di frazione che rappresenta il rapporto tra la misura sul foglio e quella sull’oggetto, ad esempio 1:100, 1:10.000, 1:50.000. Il disegno è tanto più piccolo, quanto maggiore è il denominatore della frazione. In pratica, in numeratore è sempre 1 (uno) e va sostituito con la dimensione reale dell’oggetto, espressa generalmente in centimetri, mentre al denominatore avremo il fattore di scala, ossia il valore per cui va divisa la dimensione reale.
Si scriverà ad esempio 1:5 (che si legge 1 a 5) e significa che divideremo la misura dell’oggetto per 5, ossia ridurremo di 5 volte la sua dimensione.
SCALA GRAFICA
E’ detto scala grafica quel segmento suddiviso in tante parti uguali che corrispondono alla lunghezza indicata.
 In pratica, per sapere qual’è la distanza tra due punti su una cartina geografica, basterà misurare con una squadretta la loro distanza e verificare sulla scala grafica i nostri centimetri a quanti chilometri (ad esempio) corrispondano nella realtà.
In pratica, per sapere qual’è la distanza tra due punti su una cartina geografica, basterà misurare con una squadretta la loro distanza e verificare sulla scala grafica i nostri centimetri a quanti chilometri (ad esempio) corrispondano nella realtà.
ESEMPI
Per comprendere meglio quanto detto, proviamo a fare due esempi, uno da dimensione sulla carta (dc) a dimensione reale (dr) e uno da dimensione reale a dimensione sulla carta.
Esempio 1: diciamo che due località distano tra di loro 1.2 Km nella realtà e abbiamo una planimetria della zona su carta in scala 1:10.000. Qual’è la distanza su carta? Allora, procediamo con ordine:
- convertiamo i chilometri in centimetri, quindi 1,2Km corrisponderanno a 120.000 cm;
- la scala é 1:10.000, quindi sostituiamo a 1 il valore reale in centimetri: Avremo 120.000 cm : 10.000;
- il risultato è 12 cm, ossia sulla nostra cartina 1,2Km corrispondono a 12 cm in scala 1:10.000.
Esempio 2: diciamo adesso che abbiamo misurato la distanza tra due punti su una cartina in scala 1:50.000 e che questa distanza è pari a 17 cm. Qual’è la distanza reale? Procediamo:
- l’uguaglianza per ricavare la distanza reale è la seguente: 1 : scala = distanza sulla carta : distanza reale;
- abbiamo tutto tranne la distanza reale, sostituiamo i valori: 1 : 50.000 = 17 cm : X (che si legge 1 sta a 50.000 come 17 sta a X);
- da cui X = (17 cm * 50.000) / 1;
- ossia 850.000 cm pari a 8,5Km.






 Descrivere geometricamente un oggetto significa averne interpretato la
Descrivere geometricamente un oggetto significa averne interpretato la 





 In pratica, per sapere qual’è la distanza tra due punti su una cartina geografica, basterà misurare con una
In pratica, per sapere qual’è la distanza tra due punti su una cartina geografica, basterà misurare con una